CIRCULAR  15

DE: DIRECCION EJECUTIVA CREG

PARA: TODAS LAS EMPRESAS COMERCIALIZADORAS DE

ELECTRICIDAD

REF.: ENVIO DE INFORMACION SOBRE FORMULAS TARIFARIAS DE

ELECTRICIDAD

SANTAFE DE BOGOTA,.D.C

Estimado Señor Gerente:

1. La regulación vigente ha prescrito que el Costo Base de Comercialización propuesto por cada empresa debió ser publicado por ella oportunamente.

2. El Costo Base de Comercialización C,* fijado por la CREG para cada comercializador ha sido publicado mediante la respectiva resolución. 1

3. La síntesis metodológica del modelo de eficiencia comparativa utilizado por la CREG ha sido incluida como Anexo de la resolución CREG 31 de 1997.2

Un documento de referencia con información técnica sobre el Análisis Envolvente de Datos se anexa a esta comunicación.

EDUARDO AFANADOR

Director Ejecutivo

Comisión de Regulación de Energía y Gas

1. Se encuentra en el servidor de la CREG en la respectiva resolución.

2. Esta resolución se encuentra en el servidor de la CREG.

ANEXO.

ANALISIS ENVOLVENTE DE DATOS -FUNDAMENTO TEORICO

El Análisis Envolvente de Datos o Data Envelopment Analysis (DEA) es una técnica de Optimización construida para medir el comportamiento relativo de diferentes unidades organizacionales en las cuales la presencia de múltiples insumos (inputs) y productos (outputs) hacen difícil la comparación de su desempeño. DEA provee un método para comparar la eficiencia de unidades organizacionales con respecto a las demás, en un contexto en el cual dicha eficiencia no puede ser fácilmente expresada como el cociente de un único producto sobre un único insumo, tal como lo muestra la ecuación (1):

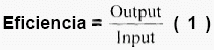
En ciertos sistemas productivos en los que hay un recurso dominante, es posible obtener con la ecuación (1) una medida de la eficiencia da cada unidad organizacional y establecer así una comparación entre las unidades para determinar cuáles son “mejores” y qué tanto podrían mejorar las otras para ser eficientes respecto a las primeras.

Sin embargo, existen sistemas en los cuales esto no es aplicable porque las unidades que conforman dicho sistema sirven diversos propósitos (que llamaremos “productos” a lo largo de este documento) y utilizan múltiples recursos (que llamaremos “insumos”), que en muchas ocasiones ni siquiera están bien definidos o que no son fácilmente cuantificables. De modo que se hace necesario establecer otra manera de medir la eficiencia de las unidades que se quiere comparar.

En estos contextos se enfrenta el problema de decidir cuál o cuáles son los criterios a utilizar para comparar la eficiencia de una unidad con respecto a otra, puesto que existen muchas medidas de desempeño o variables importantes a ser tenidas en cuenta. Es posible establecer una medida de eficiencia para cada una de las unidades, expresada de la siguiente manera:

donde t es el número de productos que se definen en la medida de eficiencia y m es el número de insumos.

Basados en dicha ecuación surge la pregunta de cómo determinar los pesos relativos que debe tener cada insumo y cada producto en la medida de eficiencia. Si se convoca a los individuos que trabajan al frente de cada una de las unidades que se desean comparar y se les solicita que determinen dichos pesos para su unidad y todas las demás, es altamente probable que los criterios de cada uno de ellos sean bastante diferentes entre si. Llegar a un consenso sobre cómo debe ser la comparación de unas unidades con otras se convierte entonces en un imposible. Cada individuo conoce la unidad en la cual trabaja, sus fortalezas y sus debilidades y por lo tanto posee un incentivo a establecer criterios que lo favorezcan.

Por otro lado, puede ocurrir que a pesar de ser sumamente objetivo en dicho análisis existan serias diferencias conceptuales o de valoración entre los individuos sobre la importancia relativa de los fines que persiguen las unidades (outputs) o de los recursos que estas usan para alcanzar dichos fines (inputs). Este asunto es crítico, porque no se trata de encontrar “la verdad” acerca de cómo debe ser el peso (o importancia) que se de a cada input o output.

Para dar una alternativa de solución a este problema se ha construido el Análisis Envolvente de Datos. Se pretende a través de esta herramienta evitar el problema de la definición exógena de los criterios para describir la eficiencia en un problema específico. Es decir, se pretende evitar que los encargados de las unidades establezcan los pesos de cada uno de los outputs y los inputs que han definido previamente.

La idea original de esta herramienta es de Charnes, Cooper y Rhodes (1978). Consiste en la construcción de un modelo de programación matemática que generaliza la definición de eficiencia técnica con un único output y un único input expresada por Farrell en 1957 (ecuación l), al caso de medir la eficiencia técnica con múltiples inputs y outputs, construyendo un cociente entre un único output “virtual” y un único input “virtual” (tal como lo expresa la ecuación 2), y en el cual los pesos son variables endógenas. De este modo, es posible realizar análisis de eficiencia técnica que permitan monitorear el desempeño de unidades organizacionales (llamadas también DMU's o Decision Making Units) en el sector público. En este sentido, el surgimiento de DEA resulta en una extensión de las metodologías de investigación de operaciones que desarrollan aplicaciones heurísticas o con métodos de optimización para resolver problemas de distribución o ubicación de recursos escasos.

Al usar DEA, se construye y resuelve un modelo de optimización para cada una de las unidades organizacionales que se van a comparar. En dicho modelo, al igual que en cualquier modelo de optimización se pretende maximizar o minimizar una función en presencia de un número determinado de restricciones. Si se desea comparar o medir la eficiencia relativa de n unidades organizacionales se construyen n modelos de optimización y en cada uno de ellos la función a maximizar es la eficiencia de la unidad organizacional j donde j varía de 1 a n (j=l,2,...n).

Las restricciones de cada uno de los n modelos son idénticas y expresan que la eficiencia de cada una de las unidades organizacionales debe ser menor que 1 (o que 100 o cualquier valor positivo), con el objetivo de que todas estén en la misma escala de medida. En otros términos, se da una cota superior a la medida de eficiencia para comprender en un contexto comparativo qué significa el hecho de que la eficiencia de una unidad tome un valor particular. Las variables de cada modelo son entonces los pesos que se deben otorgar a cada input y cada output con el objetivo de que la unidad en consideración (aquella de la cual se está tratando de maximizar su medida de eficiencia) aparezca presentada de la mejor manera posible.

El hecho de que cada uno de los n modelos que se construyen y se resuelven busque entre todos los posibles pesos a otorgar a cada input y a cada output y otorgue como resultado final los valores que hacen que cada unidad aparezca con el valor de eficiencia más alto posible tiene dos implicaciones importantes:

1. Si una unidad particular resulta ineficiente relativamente a las demás, entonces no existe otra combinación de pesos que permitan que ella obtenga un valor de eficiencia más alto. De modo que el administrador de dicha unidad organizacional no podría alegar que su unidad ha resultado ineficiente porque los pesos escogidos para los outputs y los inputs la perjudicaron.

2. Como se resuelven n modelos de optimización, los pesos que se otorgan a cada uno de los inputs y los outputs pueden resultar diferentes para las diferentes unidades. Esto resulta de la flexibilidad de la metodología pues los pesos no son determinados previamente como se hace usualmente, sino que son un resultado final.

Después de resolver todos los modelos se tienen los valores de eficiencia de todas las unidades y se puede reconocer cuáles unidades son eficientes y cuáles no. Además, se puede determinar cómo podrían “moverse” las unidades menos eficientes para mejorar, ya sea para aumentar alguno o todos sus outputs usando los mismos inputs, para producir los mismos outputs con menos inputs, o para reducir inputs y aumentar outputs simultáneamente. La manera como se mueven las unidades ineficientes hacia la frontera de eficiencia depende del modelo DEA que se utilice.

Desde 1978 a partir del desarrollo de Charnes, Cooper y Rhodes se han construido diversos modelos que son usados de acuerdo a las características de cada problema particular. Diferentes modelos pueden generar diferentes fronteras de eficiencia. Además, la proyección de una unidad ineficiente hacia la frontera varía según el modelo utilizado: En algunos de ellos, el punto proyectado en la frontera corresponde a aquel que maximiza la distancia desde el punto observado hacia el punto proyectado en la frontera en dirección noroeste; en otros, el punto proyectado corresponde al que maximiza el movimiento hacia la frontera eficiente maximizando la reducción proporcional de todos los inputs de la unidad que está siendo evaluada; en otros el punto proyectado corresponde a aquel que maximiza el movimiento de la unidad hacia la frontera eficiente maximizando el aumento proporcional de todos los outputs, etc.

El modelo usado para determinar la eficiencia relativa de las empresas de comercialización de energía eléctrica fue el siguiente:

• Modelo Lineal CCR Orientado al Producto

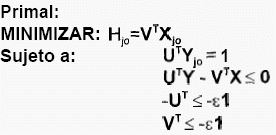
Variables:

V = Vector de los pesos otorgados a los insumos de la unidad jo.

U = Vector de los pesos otorgados a los productos de la unidad jo.

Parámetros:

X, = Vector de los niveles de los insumos de la unidad jo.

Y, = Vector de los niveles de los productos de la unidad jo.

El valor  asegura que U y V sean por lo menos iguales a un peso mínimo predefinido con el objetivo de que todos los productos e insumos considerados para la medida de eficiencia sean tenidos en cuenta.

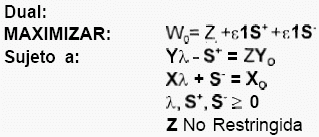
CITAS BIBLIOGRAFICAS

1 Charnes A., Cooper W. W. y Rhodes E. Measuring the Efficiency of Decision Making Units. European Journal of Operations Research, Vol. 2, pp 429-444, 1978. A'-

2 Farrell M. J. The Measurement of Productive Efficiency. Journal of the Roya1 Statistical Society. Series A (General) Part3. Vol 120, pp 252-290, 1957. /